内容不断更新,建议购买会员永久查看
什么是概率思维
概率思维,简而言之,就是借助数学和逻辑的手段,对特定事件发生的几率进行评估。这种思考方式是我们提升决策精确度的强有力工具。在这个由无数错综复杂因素交织决定的世界上,概率性思考使我们能够预测哪些结果最可能出现。一旦我们把握住了这些可能性,我们的选择就能变得更加准确、高效,从而在决策过程中游刃有余。
在商业领域,概率思维模型被用于风险评估、投资决策、市场预测等;
在科学领域,它被用于研究自然现象、社会问题等;
在体育领域,它被用于比赛策略分析、运动员表现评估等。
如何在生活中运用概率思维
深入思考我们为何需要概率思维是值得的。事物非黑即白,不是吗?我们今天要么会被雷击中,要么不会。但问题在于,只有度过这一天,我们才能得知结果,这对我们早晨做出决策并无裨益。未来并非命中注定,我们可以通过理解可能影响我们事件的发生概率来更好地应对它。
我们对世界信息的不完全掌握催生了概率理论及其实用性。我们现在明白,未来本质上是不可预测的,因为并非所有变量都能被掌握,哪怕是我们数据中的微小错误也会迅速扭曲我们的预测。我们能做的,就是通过构建切实可行的概率来预测未来。那么,我们应如何操作呢?
概率无处不在,它是世界的基础架构。我们大脑中的概率机制——由心理学家丹尼尔·卡尼曼和阿莫斯·特沃斯基提出的那些深入人心的直觉法则——是人类在计算机、工厂、交通、中层管理以及股票市场出现之前的时代进化形成的。它曾在人类生存至关重要的年代为我们服务,至今仍然发挥着重要作用。
但在今天——对大多数人而言,生存已不再是主要问题的时代,我们追求的是蓬勃发展。我们渴望竞争、渴望胜利。更重要的是,我们希望在复杂的社会系统中做出明智的决策,而这些系统并不包含在我们大脑进化出的那些(相当合理的)直觉法则之中。
因此,我们需要有意识地增强对概率的认识。这种认识是什么,我们又该如何利用它来获得优势呢?
在概率学中,有三个重要的概念我们需要理解,以便将它们融入你的思维方式中,从而提高你把握问题本质的几率:
- 贝叶斯思维
- 肥尾分布
- 不对称性
托马斯·贝叶斯与贝叶斯思维:贝叶斯是18世纪上半叶的英国牧师,他最著名的作品《求解机会论中某一问题的论文》在他去世两年后的1763年,由他的朋友理查德·普莱斯呈递给皇家学会。这篇论文,我们现在称之为贝叶斯定理的核心,探讨了我们如何在遇到新数据时调整概率。
贝叶斯思维的核心(也可以称之为贝叶斯更新)是这样的:考虑到我们对世界有有限但有用的信息,并且不断遇到新的信息,我们在学习新事物时,应当尽可能地考虑我们已经知道的信息。贝叶斯思维允许我们在做决策时利用所有相关的先前信息。统计学家可能称之为基础比率,即吸收关于你所处情境过去情况的外部信息。
设想这样一个新闻标题:“暴力事件的数量有所上升”。如果没有贝叶斯思维,你可能会真的感到害怕,因为你成为攻击或谋杀受害者的几率比几个月前要高。但贝叶斯方法会让你将这一信息放入你已经了解的关于暴力犯罪的背景中去考虑。
你知道暴力犯罪已经降至数十年来的最低水平。你现在所在的城市比这项统计开始以来的任何时候都要安全。假设去年你被刺伤的几率是万分之一,即0.01%。文章准确地指出,暴力犯罪增加了一倍。现在是万分之二,即0.02%。这真的值得我们极度担忧吗?这里的先前信息至关重要。当我们把这些信息考虑进去时,我们意识到我们的安全并没有真正受到威胁。
相反,如果我们看美国糖尿病的统计数据,我们运用先前知识的方式会引导我们得出不同的结论。在这里,贝叶斯分析表明你应该感到担忧。1958年,0.93%的人口被诊断出患有糖尿病。到了2015年,这一比例是7.4%。如果你观察这些年间的增长,你会发现糖尿病诊断的上升是稳定的,而不是一个短暂的峰值。因此,相关的先前数据或先验表明了一个令人担忧的趋势。
我们需要记住,先验本身也是概率估计。对于每一项先前的知识,你并不是将其放入一个二元结构中,判断它是真还是假。你是在给它赋予一个为真的概率。因此,你不能让先验妨碍你对新知识的处理。在贝叶斯术语中,这称为似然比或贝叶斯因子。任何你遇到的挑战先验的新信息,简单地意味着那个先验为真的概率可能降低了。最终,一些先验可能会被完全替代。这是一个不断挑战和验证你所认为你知道的东西的循环。在做出不确定的决策时,几乎总是一个错误不问:相关的先验是什么?我已经知道的东西中有哪些可以用来更好地理解情况的现实?
现在我们需要来看肥尾分布曲线:我们中的许多人都熟悉正态分布曲线,那个美妙的、对称的波形,捕捉了从身高到考试成绩等诸多事物的相对频率。正态分布曲线之所以伟大,是因为它易于理解和使用。它的专业名称是“正态分布”。如果我们知道自己处于一个正态分布的情况中,我们可以迅速确定我们的参数,并为最可能的结果做计划。
肥尾分布曲线则有所不同。请看:
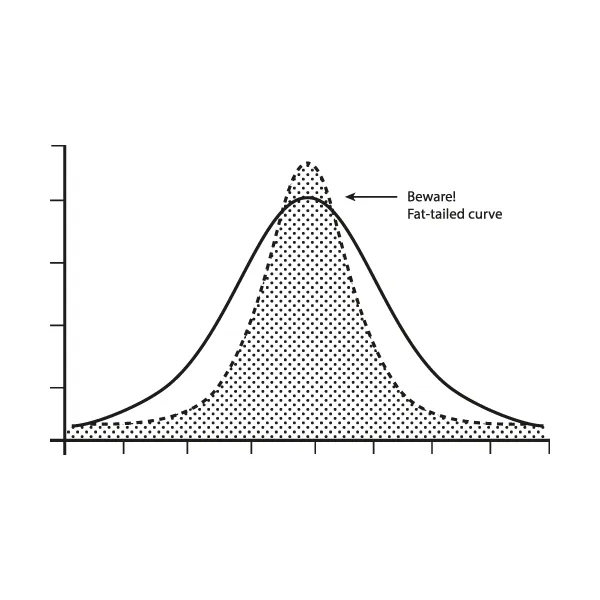
初看之下,它们似乎颇为相似。常见结果聚集在一起,形成一股波动。区别在于两端的尾部。在正态分布曲线中,极端情况是可预测的。偏离均值的程度总有一个限度。而在肥尾分布曲线中,极端事件并没有真正的上限。
可能发生的极端事件越多,曲线的尾部就越长。尽管任何一个极端事件仍然不太可能发生,但众多可能性意味着我们不能仅仅依赖最常见的结果来代表平均水平。可能发生的极端事件越多,它们发生的概率就越大。不可思议的事情肯定会发生,我们却无法预知何时会发生。
可以这样想:在正态分布的情况下,比如展示人类身高或体重的分布,可能性的光谱上有异常值,但这些异常值有一个相当明确的定义范围。你永远不会遇到一个比普通人大十倍的人。但在肥尾分布曲线中,比如财富分布,中心趋势并不以同样的方式运作。你可能会经常遇到比普通人富裕十倍、百倍甚至万倍的人。那是一个截然不同的世界。
让我们重新审视我们之前在贝叶斯思维背景下讨论的暴力风险的例子。假设你听说,与死于恐怖主义相比,你在楼梯上滑倒并摔破脑袋的风险更大。统计数据和先验知识似乎支持这一观点:去年你的国家有1000人因楼梯滑倒死亡,而只有500人死于恐怖主义。你应该更担心楼梯还是恐怖事件?
有些人用这样的例子来证明恐怖风险很低——既然近期死亡人数很少,为什么要担心?问题在于尾部的厚度:恐怖暴力的风险更像是财富分布,而楼梯滑倒死亡则更像是身高和体重的分布。在未来十年中,可能发生多少事件?尾部有多厚?
重要的是不要坐下来想象尾部中所有可能的情景(按定义,这是不可能的),而是要以正确的方式处理肥尾分布的领域:通过定位自己来生存甚至从极度不可预测的未来中获益,通过成为唯一正确思考并为一个我们不完全理解的世界制定计划的人。
不对称性:最后,你需要考虑我们可能称之为“元概率”的东西——即你的概率估计本身有多准确的概率。
这个被严重误解的概念与不对称性有关。如果你看专业投资者精心准备的股票推介,几乎每次提出一个想法时,投资者都会注视着听众的眼睛,并声明他们认为自己将实现每年20%至40%甚至更高的回报率。然而,很少有人能达到这个标准,并不是因为他们没有赢家。而是因为他们猜错了太多。他们一贯高估了自己对概率估计的信心。(作为参考,在美国,长期来看,普通股市的年回报率不超过7%至8%,这还是扣除费用之前的数字。)
另一个常见的不对称性是人们对交通对旅行时间影响的估计。你有多少次数着“准时”出发却提前20%的时间到达?几乎从没有?你有多少次数着“准时”出发却晚到20%?总是这样?没错。你的估计错误是不对称的,偏向单一方向。这在概率决策中很常见。
在“过于乐观”的错误估计方面,比“过于悲观”的错误估计要多得多。你很少会读到一个投资者目标是每年25%的回报率,而长期实际获得的收益却达到了40%。相反,如果你随机往《华尔街日报》上投掷飞镖,很可能会戳中那些目标为年化收益率为25%的投资者,但他们最终得到的结果往往只有10%左右。
总结
掌握概率思维意味着我们能够辨识关键因素,对事件发生的概率有所把握,审视并验证我们的假设,进而做出明智的决策。在充满变数和不确定性的环境中,这种思维方式使我们能够更有信心地采取行动。虽然我们无法绝对准确地预知未来,但概率思维却是一种极为宝贵的工具,它帮助我们预测未来可能的发展趋势,并据此制定出有效的应对策略。通过这种方式,我们能更好地适应变化,把握机遇,规避风险。
在商业领域,概率思维模型被用于风险评估、投资决策、市场预测等;
【点击查看社群介绍】加入曹哲万人成长社群,装备专属你的成长智库:这个世界一切都有了,您只需要把它找到,用就行了!
隐藏内容为会员内容,想改变先学会付费。先看免费内容,有收获再付费。前1000名200元终身,满额后改为年费。会员务必加微信,拉入群内分享更多精彩内容。






暂无评论内容